Определение сложности алгоритмов в Python с Big-O Notation

6633

Определение сложности алгоритмов в Python с Big-O Notation

Big-O Notation

Во время разработки программы у программиста, зачастую, есть несколько способов решения одной и той же задачи. Например, если стоит цель отсортировать элементы в массиве, это можно сделать с помощью сортировки слиянием, сортировки вставкой или несколькими другими методами. Очевидно, что каждый алгоритм имеет свои плюсы и минусы, но в первую очередь разработчик должен выбрать наиболее эффективный.

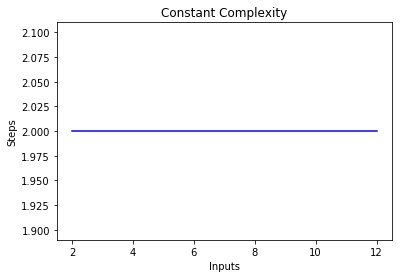
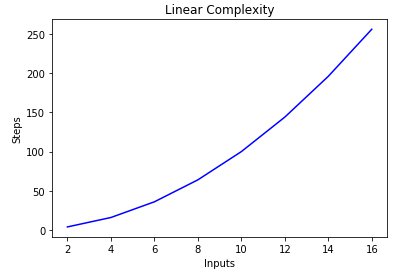
Для поиска оптимального решения при разработке на Python принято использовать Big-O Notation — статистическую меру определения сложности алгоритма.

В этой статье рассмотрим, почему в своей работе стоит использовать именно Big-O нотацию, и как ее применять на практике с помощью различных функций Python.

Способы определения сложности алгоритма

Чтобы понять, как правильно определить сложность алгоритма, рассмотрим практический пример. Допустим, перед нами стоит задача разработать программу на языке Python, которая будет вычислять факториал от заданного пользователем числа. Здесь есть как минимум два пути решения. Рассмотрим оба.

В первом случае создадим функцию fact с переменной product, которая будет запускаться со значением 1. Дальше запустим цикл for, который будет перебирать значения от 1 до N, и во время каждой итерации умножать значение в product на число, повторяемое циклом, с последующим сохранением полученного значения в product. Возвращая product в конце функции мы получим факториал.

В коде это будет выглядеть так:

def fact(n):
  product = 1
  for i in range(n):
     product = product * (i + 1)
return product
print (fact(5))

Во втором варианте реализации используем рекурсивную функцию. Код будет выглядеть так:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

Чтобы решить, какой вариант использовать в своей программе нужно определить сложность алгоритма. Самый очевидный ответ — измерить время, затрачиваемое на решение каждого алгоритма, что можно сделать с помощью литерала %time it. В первом варианте мы получим 9 микросекунд на цикл, а во втором — 15 микросекунд. Но если вы попробуете выполнить проверку на своем устройстве, то цифры могут отличаться.

Это говорит о том, что секунды, минуты и часы — не самые объективные показатели сложности, поскольку скорость работы алгоритма зависит от железа и множества других внешних факторов. Поэтому, чтобы избежать погрешностей, которые могут привести к проблемам с производительностью ПО, принято использовать более точные метрики. Вот тут возникает необходимость в Big-O нотации.

Принцип анализа алгоритмов с нотацией Big-O

Для применения Big-O Notation в коде Python используется простой синтаксис, где большая буква «О» обозначает запуск нотации, а в круглых скобках после нее указывается нужная функция.

Вот наиболее распространенные функции Big-O:

Постоянная — O(c);
Линейная — O(n);
Квадратная — O(n^2);
Кубическая — O(n^3);

Экспонентная — O(2^n);
Логарифмическая — O(log(n));
Логарифмическая линейная — O(nlog(n)).

На практике, если между входными данными и шагом, который выполняет алгоритм, есть линейная зависимость, нужно использовать линейную нотацию — O(n), а если квадратичная — соответственно O(n^2).

Чтобы понять, какую именно нотацию Big-O в Python нужно использовать в конкретном случае, рассмотрим несколько практических примеров.

Постоянная сложность — O(c)

Сложность алгоритма считается постоянной в случаях, когда для его выполнения нужно фиксированное количество шагов, вне зависимости от объема входных данных. В такой ситуации для определения сложности нужно использовать постоянную функцию нотации Big-O — O(c).

В качестве примера создадим небольшой алгоритм, который вычисляет квадрат первого элемента в списке, а затем выводит на экран полученное значение:

def constant_algo(items):
    result = items[0] * items[0]
    print()
    
constant_algo([4, 5, 6, 8])

Как видим, алгоритму неважен размер введенного значения. Он выполняет только три действия:

находит первый элемент в списке;
возводит его во вторую степень;
выводит на экран полученное значение.

Значит мы можем уверенно сказать, что у нас постоянная сложность. Чтобы убедиться в этом окончательно, можно нарисовать линейный график с плавающим размером входных данных items на оси X и количеством необходимых шагов на оси Y.

Для визуализации напишем такой сценарий:

import matplotlib.pyplot as plt
import numpy as np

x = [2, 4, 6, 8, 10, 12]

y = [2, 2, 2, 2, 2, 2]

plt.plot(x, y, 'b')
plt.xlabel('Inputs')
plt.ylabel('Steps')
plt.title('Constant Complexity')
plt.show()

На выходе получим еще одно подтверждение того, что сложность постоянна:

Линейная сложность — O(n)

В алгоритме с линейной сложностью количество шагов, необходимых для его выполнения пропорционально увеличивается или уменьшается в зависимости от количества входных данных. Для работы с линейной функцией Big-O Notation нужно использовать O(n).

Для примера создадим алгоритм, который будет выводить в консоль все элементы списка:

def linear_algo(items):
    for item in items:
        print(item)
        
linear_algo([4, 5, 6, 8])

Количество итераций нашего цикла for будет напрямую зависеть от длины входного массива — если в нем 4 items, значит будет 4 итерации, соответственно если мы дадим на входе 10 items, будет 10 итераций. Таким образом можно констатировать линейную сложность функции linear_algo.

Однако в этом примере есть небольшой нюанс. Если на входе будет очень большое количество данных, константы окажутся незначительными.

Рассмотрим такой пример:

def linear_algo(items):
    for item in items:
        print(item)
        
    for item in items:
        print(item)

        
linear_algo([4, 5, 6, 8])

Здесь мы видим два цикла for, которые работают с исходным списком items. Соответственно, сложность нашего алгоритма становится O(2n). Но в случае бесконечных элементов на входе, мы получаем удвоение бесконечности, которое равняется бесконечности. Следовательно мы можем игнорировать вторую константу и работать со сложностью O(n).

Квадратичная сложность — O(n^2)

Квадратичная сложность алгоритма возникает в случаях, когда необходимое количество шагов для выполнения алгоритма равняется квадратичной функции количества элементов на входе. Она обозначается O(n^2).

Рассмотрим пример функции с квадратичной сложностью. Для этого создадим сценарий с двумя циклами, где первый первый for обрабатывает все элементы входного списка, а затем передает полученные значения во вложенный for.

Пример кода:

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, '', item)
            
            
quadratic_algo([4, 5, 6, 8])

В результате мы получаем * n количество шагов, где n равняется количеству элементов в исходном массиве.

График для алгоритма с квадратичной сложностью будет выглядеть следующим образом:

Определение сложности для сложных функций

Во всех примерах выше у нас была только одна функция, поэтому определить сложность алгоритма было довольно просто. Однако в «боевых» проектах такое случается довольно редко.

Рассмотрим, как правильно определить сложность алгоритма в случаях, когда в нем задействованы сразу несколько функций.

Для этого создадим небольшой пример:

def complex_algo(items):
    for i in range(5):
        print("Python is awesome")
        
    for item in items:
        print(item)
        
    for item in items:
        print(item)
        
        
    print("Big 0")
    print("Big 0") 
    print("Big 0") 
    
    
    
complex_algo([4, 5, 6, 8])

В этом скрипте выполняется сразу несколько задач:

оператор print выводит в консоли строку 5;
исходный список дважды печатается на экране;
еще одна строка трижды выводится в консоль.

Чтобы найти сложность такого алгоритма, в первую очередь нужно разделить код на части, а уже после этого выяснить сложность каждой из них. Сделаем это на практике.

В первой части у нас получится:

for i in range(5):
    print("Rython is awesome")

Ее сложность будет O(5), поскольку здесь постоянная сложность, которая не зависит от объема входных данных.

Вторая часть:

for item in items:
        print(item)

Здесь мы видим линейную зависимость, поэтому сложность будет O(n). Соответственно, такая ж сложность будет и у следующего фрагмента кода:

Пример кода:

for item in items:
        print(item)

В последнем фрагменте строка печатается три раза, значит у нас снова постоянная сложность, которая равняется O(3).

Чтобы определить общую сложность скрипта, нам остается только суммировать полученные значения:

Пример:

0(5) + 0(n) + 0(n) + 0(3)

В упрощенном варианте это будет иметь такой вид:

0(8) + 0(2n)

Здесь мы столкнулись с нюансом, который подробно разбирали выше — наш вход с длинной n стал чрезвычайно большим, а значит мы можем игнорировать константы, ведь дважды бесконечность или половина бесконечности, все равно остаются бесконечностью. В итоге окончательная сложность этого скрипта будет O(n).

Сложность худшего и лучшего случая

Реальная и предполагаемая сложность алгоритма могут отличаться, и зачастую рассматривается два варианта — лучший и худший. Посмотрим, как это выглядит на практике.

Допустим у нас есть такой скрипт:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            return False
            
            
num = [2, 4, 6, 8, 10]

Здесь мы видим функцию, которая принимает число и массив чисел в качестве исходных данных. Если переданное число найдено в массиве — возвращается true, а если нет — false.

Например, если мы ищем число 2, которое в массиве первое для сравнения, то получим наилучший случай сложности алгоритма — O(1). Если же искомый элемент будет последним в массиве, скрипту придется перебирать все числа, и соответственно сложность возрастет до O(n) — это будет худшая сложность.

Сложность пространства

Кроме прочего, при написании кода на Python разработчик может определить пространственную сложность, которая отражает объем оперативной памяти, который необходим для выполнения программы.

Рассмотрим такой пример:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)
    return square_list
    
    
nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Здесь функция получает список целых чисел, а затем возвращает его со значениями, возведенными во вторую степень. Для работы такого алгоритма будет использован объем памяти, пропорциональный количеству элементов исходного массива, а значит пространственная сложность будет линейной O(n).

Практика по Big-O Notation и изучение Python

Если вы хотите освоить язык программирования Python и, в частности, научиться пользоваться Big-O Notation на практических примерах — присоединяйтесь к курсам в лаборатории SpaceLAB. У нас обучение проходит полностью бесплатно, под кураторством опытных менторов. Кроме того, наиболее успешные студенты получают реальную возможность трудоустройства в AVADA MEDIA — одну из лучших IT-компаний Украины.