Визначення складності алгоритмів у Python з Big-O Notation

6845

Визначення складності алгоритмів у Python з Big-O Notation

Про Big-O Notation

Під час розробки програми у програміста найчастіше є кілька способів вирішення однієї й тієї ж задачі. Наприклад, якщо варто відсортувати елементи в масиві, це можна зробити за допомогою сортування злиттям, сортування вставкою або декількома іншими методами. Очевидно, кожен алгоритм має свої плюси і мінуси, але в першу чергу розробник повинен вибрати найбільш ефективний.

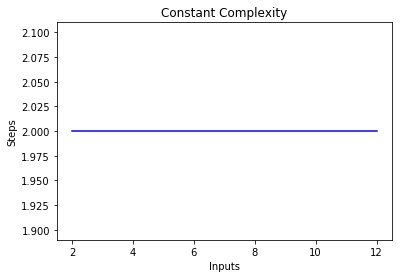
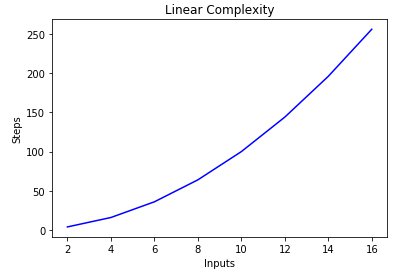
Для пошуку оптимального рішення при розробці Python прийнято використовувати Big-O Notation — статистичну міру визначення складності алгоритму.

У цій статті розглянемо, чому у своїй роботі варто використовувати саме Big-O Notation і як її застосовувати на практиці за допомогою різних функцій Python.

Способи визначення складності алгоритму

Щоб зрозуміти, як правильно визначити складність алгоритму, розглянемо приклад. Припустимо, перед нами стоїть завдання розробити програму мовою Python, яка обчислюватиме факторіал від заданого користувачем числа. Тут є як мінімум два шляхи вирішення. Розглянемо обидва.

У першому випадку створимо функцію fact зі змінною product, яка запускатиметься зі значенням 1. Далі запустимо цикл for, який буде перебирати значення від 1 до N, і під час кожної ітерації множити значення в product на число, повторюване циклом, з подальшим збереженням отриманого значення в product. Повертаючи продукцію в кінці функції ми отримаємо факторіал.

У коді це виглядатиме так:

def fact(n):
  product = 1
  for i in range(n):
     product = product * (i + 1)
return product
print (fact(5))

У другому варіанті реалізації використовуємо рекурсивну функцію. Код виглядатиме так:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

Щоб вирішити, який варіант використовувати у своїй програмі, потрібно визначити складність алгоритму. Найочевидніша відповідь — виміряти час, що витрачається рішення кожного алгоритму, що можна зробити з допомогою літералу %time it. У першому варіанті ми отримаємо 9 мікросекунд на цикл, а в другому – 15 мікросекунд. Але якщо ви спробуєте виконати перевірку на своєму пристрої, цифри можуть відрізнятися.

Це говорить про те, що секунди, хвилини та години — не найоб'єктивніші показники складності, оскільки швидкість роботи алгоритму залежить від заліза та багатьох інших зовнішніх факторів. Тому, щоб уникнути похибок, які можуть призвести до проблем із продуктивністю ПЗ, прийнято використовувати більш точні метрики. Ось тут виникає потреба у Big-O нотації.

Принцип аналізу алгоритмів із нотацією Big-O

Для застосування Big-O Notation у коді Python використовується простий синтаксис, де велика літера «О» позначає запуск нотації, а круглих дужках після неї вказується потрібна функція.

Ось найпоширеніші функції Big-O:

Постійна - O(c);
Лінійна - O(n);
Квадратна - O(n ^ 2);
Кубічна - O(n ^ 3);

Експонентна - O(2^n);
Логарифмічна - O(log(n));
Логарифмічна лінійна - O(nlog(n)).

Насправді, якщо між вхідними даними та кроком, який виконує алгоритм, є лінійна залежність, потрібно використовувати лінійну нотацію — O(n), і якщо квадратична — відповідно O(n^2).
Щоб зрозуміти, яку саме нотацію Big-O у Python потрібно використовувати у конкретному випадку, розглянемо кілька практичних прикладів.

Постійна складність - O(c)

Складність алгоритму вважається постійною у випадках, коли для його виконання потрібна фіксована кількість кроків, незалежно від обсягу вхідних даних. У такій ситуації для визначення складності необхідно використовувати постійну функцію нотації Big-O - O(c).

Як приклад створимо невеликий алгоритм, який обчислює квадрат першого елемента у списку, а потім виводить на екран отримане значення:

def constant_algo(items):
    result = items[0] * items[0]
    print()
    
constant_algo([4, 5, 6, 8])

Як бачимо, алгоритм неважливий розмір введеного значення. Він виконує лише три дії:

знаходить перший елемент у списку;
зводить його на другий ступінь;
виводить на екран отримане значення.

Отже, ми можемо впевнено сказати, що у нас постійна складність. Щоб переконатися в цьому остаточно, можна намалювати лінійний графік із плаваючим розміром вхідних даних items на осі X та кількістю необхідних кроків на осі Y.

Для візуалізації напишемо такий сценарій:

import matplotlib.pyplot as plt
import numpy as np

x = [2, 4, 6, 8, 10, 12]

y = [2, 2, 2, 2, 2, 2]

plt.plot(x, y, 'b')
plt.xlabel('Inputs')
plt.ylabel('Steps')
plt.title('Constant Complexity')
plt.show()

На виході отримаємо ще одне підтвердження того, що складність стала:

Лінійна складність - O(n)

У алгоритмі з лінійною складністю кількість кроків, необхідні його виконання пропорційно збільшується чи зменшується залежно кількості вхідних даних. Для роботи з лінійною функцією Big-O Notation необхідно використовувати O(n).

Для прикладу створимо алгоритм, який виводитиме в консоль усі елементи списку:

def linear_algo(items):
    for item in items:
        print(item)
        
linear_algo([4, 5, 6, 8])

Кількість ітерацій нашого циклу for безпосередньо залежатиме від довжини вхідного масиву - якщо в ньому 4 items, значить буде 4 ітерації, відповідно якщо ми дамо на вході 10 items, буде 10 ітерацій. Таким чином, можна констатувати лінійну складність функції linear_algo.

Однак у цьому прикладі є невеликий нюанс. Якщо на вході буде дуже багато даних, константи виявляться незначними.

Розглянемо такий приклад:

def linear_algo(items):
    for item in items:
        print(item)
        
    for item in items:
        print(item)

        
linear_algo([4, 5, 6, 8])

Тут ми бачимо два цикли for, які працюють з вихідним списком елементів. Відповідно, складність нашого алгоритму стає O(2n). Але у випадку нескінченних елементів на вході ми отримуємо подвоєння нескінченності, яке дорівнює нескінченності. Отже, ми можемо ігнорувати другу константу і працювати зі складністю O(n).

Квадратична складність - O(n^2)

Квадратична складність алгоритму виникає у випадках, коли необхідна кількість кроків до виконання алгоритму дорівнює квадратичної функції кількості елементів на вході. Вона позначається O(n^2).

Розглянемо приклад функції із квадратичною складністю. Для цього створимо сценарій з двома циклами, де перший перший for обробляє всі елементи вхідного списку, а потім передає отримані значення вкладений for.

Приклад коду:

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, '', item)
            
            
quadratic_algo([4, 5, 6, 8])

В результаті ми отримуємо * n кількість кроків, де дорівнює кількості елементів у вихідному масиві.

Графік для алгоритму з квадратичною складністю виглядатиме так:

Визначення складності для складних функцій

У всіх прикладах вище у нас була лише одна функція, тому визначити складність алгоритму було досить легко. Однак у «бойових» проектах таке трапляється досить рідко.

Розглянемо, як правильно визначити складність алгоритму у випадках, коли у ньому задіяно відразу кілька функцій.

Для цього створимо невеликий приклад:

def complex_algo(items):
    for i in range(5):
        print("Python is awesome")
        
    for item in items:
        print(item)
        
    for item in items:
        print(item)
        
        
    print("Big 0")
    print("Big 0") 
    print("Big 0") 
    
    
    
complex_algo([4, 5, 6, 8])

У цьому скрипті виконується відразу кілька завдань:

оператор print виводить у консолі рядок 5;
вихідний список двічі друкується на екрані;
ще один рядок тричі виводиться у консоль.

Щоб знайти складність такого алгоритму, в першу чергу потрібно розділити код на частини, а після цього з'ясувати складність кожної з них. Зробимо це практично.

У першій частині у нас вийде:

for i in range(5):
    print("Rython is awesome")

Її складність буде O(5), оскільки тут постійна складність, яка залежить від обсягу вхідних даних.

Друга частина:

for item in items:
        print(item)

Тут бачимо лінійну залежність, тому складність буде O(n). Відповідно, така ж складність буде і в наступного фрагмента коду:

Приклад коду:

for item in items:
        print(item)

В останньому фрагменті рядок друкується три рази, отже, у нас знову постійна складність, яка дорівнює O(3).

Щоб визначити загальну складність скрипту, нам залишається лише підсумовувати отримані значення:

Приклад:

0(5) + 0(n) + 0(n) + 0(3)

У спрощеному варіанті це матиме такий вигляд:

0(8) + 0(2n)

Тут ми зіткнулися з нюансом, який докладно розбирали вище — наш вхід з довгою n став надзвичайно великим, а значить ми можемо ігнорувати константи, адже двічі нескінченність чи половина нескінченності все одно залишаються нескінченністю. У результаті остаточна складність цього сценарію буде O(n).

Складність гіршого та кращого випадку

Реальна та передбачувана складність алгоритму можуть відрізнятися, і найчастіше розглядається два варіанти – найкращий та найгірший. Подивимося, як це на практиці.

Допустимо у нас є такий скрипт:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            return False
            
            
num = [2, 4, 6, 8, 10]

Тут ми бачимо функцію, яка приймає число та масив чисел як вихідні дані. Якщо передане число знайдено в масиві, повертається true, а якщо ні — false.

Наприклад, якщо ми шукаємо число 2, яке в масиві перше для порівняння, отримаємо найкращий випадок складності алгоритму — O(1). Якщо ж потрібний елемент буде останнім у масиві, скрипту доведеться перебирати всі числа, і відповідно складність зросте до O(n) — це буде найгірша складність.

Складність простору

Крім того, при написанні коду на Python розробник може визначити просторову складність, яка відображає обсяг оперативної пам'яті, необхідний для виконання програми.

Розглянемо такий приклад:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)
    return square_list
    
    
nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

Тут функція отримує список цілих чисел, а потім повертає його зі значеннями, зведеними на другий ступінь. Для роботи такого алгоритму буде використано обсяг пам'яті, пропорційний кількості елементів вихідного масиву, а значить просторова складність буде лінійною O(n).

Практика з Big-O Notation та вивчення Python

Якщо ви хочете освоїти мову програмування Python і, зокрема, навчитися користуватися Big-O Notation на практичних прикладах, приєднуйтесь до курсів у лабораторії SpaceLAB. У нас навчання відбувається повністю безкоштовно, під кураторством досвідчених менторів. Крім того, найуспішніші студенти отримують реальну можливість працевлаштування в AVADA MEDIA – одну із найкращих IT-компаній України.